Gibbsova energie (FBLT)

Rozdíl chemických potenciálů produktů a reaktantů souvisí s termodynamickou funkcí nazývanou změna Gibbsovy energie (ΔG). Z mnoha možných definic Gibbsovy energie jsou pro biochemii důležité dvě:

1. Změna Gibbsovy energie je rovna maximálnímu množství (neobjemové) práce, kterou může systém vykonat;
2. Změna Gibbsovy energie je mírou vychýlení se od rovnovážného stavu.

První definice nám říká, že ΔG můžeme použít k předpovědi, zda k reakci dojde a jestli ji lze využít jako zdroj energie pro jiné procesy (svalová kontrakce, přesun iontů přes membránu).

Druhá definice vyjadřuje dva fakty:

a) v rovnovážném stavu se ΔG rovná nule;

b) změna koncentrací látek v systému, který není v rovnováze, změní (zvýší nebo sníží) ΔG.

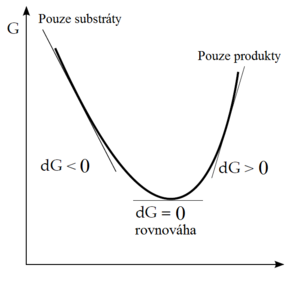
Smysl změny Gibbsovy energie se dá ilustrovat i následujícím zobrazením:

Pokud reakce začne jen se směsí reaktantů, bude probíhat směrem k produktům tak dlouho, dokud bude ΔG negativní. Nabude-li chemický potenciál produktů stejné hodnoty jako u reaktantů, systém dosáhl stavu nejnižší energie a reakce se zastaví. Reakční směs je nyní v rovnováze. Nedá se předpokládat, že by reakce pokračovala dál, protože ΔG je v další části křivky pozitivní.

Platí tedy:

ΔG < 0 – reakce probíhá spontánně;

ΔG = 0 – rovnovážný stav;

ΔG > 0 – reakce spontánně neprobíhá.

Změnu Gibbsovy energie můžeme také definovat prostřednictvím termodynamických veličin jako entalpie (H) a entropie (S):

(5)

ΔG = ΔH – T · ΔS

Změna entalpie je energie uvolněná nebo spotřebovaná během reakce (negativní hodnota znamená uvolnění energie a naopak).

Entropie se často považuje za míru neuspořádanosti systému. Podle druhého zákona termodynamiky neuspořádanost (a tedy i entropie) všech uzavřených systémů narůstá.

Z rovnice (5) vyplývá, že chemická reakce může být poháněna (tzn. dosáhnout negativní ΔG) buď vhodnou (tedy negativní) změnou entalpie, nebo dostatečným nárůstem entropie, či oběma současně.

Z praktických důvodů je vhodné definovat standardní podmínky, za nichž se ΔG a jiné veličiny změří, a poté je použít k výpočtům za skutečných situací. V chemii se považují za standardní podmínky tlak 101 325 Pa, teplota 25 °C (298,15 K) a jednotková aktivita (zjednodušeně tedy jednomolární koncentrace všech látek). Veličiny, které v těchto podmínkách změříme, se označují indexem ⁰. Biochemici definují své standardní podmínky při neutrálním pH, standardní veličiny jsou pak značeny s čárkou: ′.

Z tabulkových hodnot ΔG⁰ nebo ΔG⁰′ můžeme vypočítat ΔG pro jakoukoliv reakci pomocí rovnice:

(6)

$\Delta G=\Delta G^{0}+R\cdot T\cdot ln{\frac {[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}}$

V rovnovážném stavu je ΔG rovné nule a výraz  ${\frac {[C]^{c}\cdot [D]^{d}}{[A]^{a}\cdot [B]^{b}}}$  je roven rovnovážné konstantě K_eq.

Rovnice (6) tedy v rovnovážném stavu nabývá podoby:

(7)

ΔG = −R · T · ln K_eq

Prostřednictvím této rovnice pak můžeme vypočítat rovnovážnou konstantu z ΔG či naopak.

Snadná dostupnost hodnot ΔG⁰ může vést k uspěchaným závěrům o nemožnosti průběhu reakce při nalezení pozitivních hodnot ΔG⁰ v tabulkách. Tomu je ale třeba se vyhnout.

Ukažme si to na následujícím příkladu: Metabolická dráha glykolýzy obsahuje krok, ve kterém dochází k přeměně glukóza-6-fosfátu na izomer, fruktóza-6-fosfát. ΔG0‘ této reakce činí +1,7 kJ/mol. Znamená to tedy, že naše buňky prováděním této reakce každou sekundu našeho života porušují zákony termodynamiky?

Je důležité mít na paměti rozdíl mezi ΔG a ΔG⁰ a ΔG⁰‘. Jen samotné ΔG nám může prozradit něco o termodynamickém profilu konkrétní reakce. Hodnoty ΔG⁰ a ΔG⁰‘ platí jen při zachování standardních podmínek, které ale jsou v přírodě velmi zřídka (jestli vůbec) přítomny. Abychom mohli posoudit pravděpodobnost, že k reakci dojde, musíme znát skutečné koncentrace všech látek, jež se jí účastní.

V našem případě enzymů dochází jejich činností k neustálému odstraňování fruktóza-6-fosfátu, a tak se jeho koncentrace udržuje nízká. Celkové ΔG izomerizace Glc-6-P na Fru-6-P je díky tomu za podmínek, které jsou v buňce, záporné (−2,5 kJ/mol). Vidíme tedy, že mohou probíhat i některé energeticky relativně nepříznivé reakce, jsou-li sdruženy s reakcemi energeticky příznivými (v tomto případě těmi, které odčerpávají produkty nebo dodávají reaktanty).

Pokud reakce přeměny A → B dosahuje rovnovážného stavu s nízkou koncentrací látky B, můžeme ji sdružit s reakcí přeměny B → C, která naopak dosahuje rovnovážného stavu pouze při nízkých koncentracích reaktantu B. Druhá reakce potom efektivně odstraňuje látku B tvořenou první reakcí a brání jí tak v dosažení rovnovážného stavu.

V našem příkladu glykolýzy enzym fosfofruktokináza velmi efektivně fosforyluje Fru-6-P na fruktózu-1,6-bisfosfát, čímž zamezuje hromadění Fru-6-P, který by předchozí reakci brzdil.