ANOVA

Analýza rozptylu (variance), z anglického pojmu Analysis of variance, je druh statistického testování hypotéz. Užíváme ji pro testování hypotéz setávající z více než dvou sledovaných skupin, u nichž známe střední hodnotu. Studentův t-test je analýze rozptylu podobný, ale aplikuje se pro testování pouze dvou výběrů.

Nulová hypotéza $H_{0}$ předpokládá, že všechny skupiny mají stejnou střední hodnotu. Alternativní hypotéza $H_{1}$ naopak předpokládá, že střední hodnoty jsou odlišné.

Mnoho testů pro srovnání charakteristik námi zkoumaných výběrů jsou založeny na porovnávání dvou skupin. V praxi se ale často stává, že nám dvě skupiny nestáčí a potřebujeme srovnat skupin více. Samožrejmě lze (mějme například tři různé skupiny) testovat dvě skupiny (první s druhou), pak další dvě (druhou s třetí) a další dvě (třetí s první). Je nutné si ale uvědomit, že s rostoucím počtem testovaných hypotéz roste pravděpodobnost falešně pozitivního výsledku. V každém tomto testování je 95% pravděpodobnost, že neuděláme statistikou chybu I. chybu, tedy že nesprávně zamítneme nulovou hypotézu ve prospěch hypotézi alternativní. Pokud jsou tedy provedeny tři testy, tato pravděpodobnost bude Nelze pochopit (syntaktická chyba): {\displaystyle 0,95 × 0,95 × 0,95 = 0,857} , tedy o přibližně 10 % vyšší než v případě testování pouze jednoho. Z tohoto důvodu je vhodné použít parametrický test vhodný pro více než dva výběry.

Klasifikace

Vstupním proměnným (základní rozdělení do skupin) říkáme faktory, jedná se o kategoriální data. Na základě počtu faktorů rozdělujeme možnosti samotné analýzy:

1. jednofaktorová ANOVA (one-way ANOVA) = máme pouze jeden faktor, například pohlaví (muž, žena);
2. dvoufaktorová ANOVA (two-way ANOVA) = faktorů máme více, například faktor pohlaví a faktor vzdělání, kdy jejich kombinace vytváří celkem šest skupin;
3. vícefaktorová ANOVA (n-way ANOVA) = více než dva faktory.

Základní předpoklady

Abychom mohli analýzu rozptylu provést, je nutné zjistit, zda:

1. jsou hodnoty sledované veličiny na sobě vzájemně nezávislé a zda jsou normálně rozložené;
2. mají srovnatelný rozptyl $\sigma ^{2}$.

Pokud tyto podmínky splněny nejsou, je nutné použít neparametrické testy, které neuvažují normálně rozdělené hodnoty, jedinou podmínkou je, že musí být spojité. Jednofaktorová neparametrická ANOVA pro nezávislá měření se nazývá Kruskal-Wallis test, v případě závislých měření se používá Friedmanův test.

Příklad

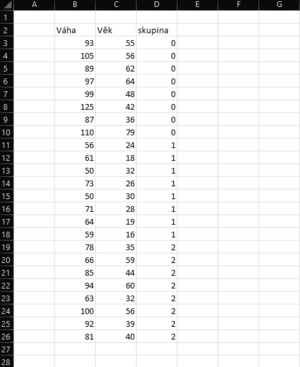
Představme si, že máme celkem 24 osob s hepatitidou. Těchto 24 pacientů rozdělíme do tří skupin: jedna skupina budou osoby s infekční hepatitidou, jedna s autoimunitní a jedna s toxickou hepaptitidou. U každé této skupiny chceme zjistit, jak (zda) se liší střední hodnota jejich věku a váhy.

Provádět pro jednoduchost budeme dvě jednofaktorové analýzy rozptylu – jednu pro věk a jednu pro váhu.

Nejjednodušší je zanést si hodnoty do souhrnné tabulky následujícím způsobem, kdy skupina 0 = pacienti s infekční hepatitidou, skupina 1 = pacienti s autoimunitní hepatitidou a skupina 2 = pacienti s toxickou hepatitidou (naše vstupní data, kategoriální, tedy zmiňovaný faktor).

Navrhněme si proto dvě tabulky, jednu pro věk a jednu pro váhu jednotlivých osob rozdělených ve třech skupinách:

Charakteristiky skupin podle věku (roky)

Infekční hepatitida	Autoimunitní hepatitida	Toxická hepatitida
55	24	35
56	18	59
62	32	44
64	26	60
48	30	32
42	28	56
36	19	39
79	16	40

Charakteristiky skupin podle váhy (kg)

Infekční hepatitida	Autoimunitní hepatitida	Toxická hepatitida
93	56	78
105	61	66
89	50	85
97	73	94
99	50	63
125	71	100
87	64	92
110	59	81

Výpočet

Abychom samotnou analýzu rozptylu mohli provést, je nutné zjistit, zda jsou naše data normálně rozdělená – pro zjednodušení test normality v našem příkladu provádět nebudeme, v praxi je ale nutné jej udělat.

Pro výpočet zavádíme tři tzv. odhady variability.

Porovnání průměrů váhy napříč zkoumanými skupinami s jasně statisticky signifikantním rozdlem p<0,001, kdy zamítáme nulovou hypotézu ve prospěch hypotézy alternativní.

Porovnání průměrů věku napříč zkoumanými skupinami s jasně statisticky signifikantním rozdlem p<0,001.

1. Celkový počet čtverců (tzv. total sum of squares), $S_{T}$ = charakterizuje celkovou variabilitu v daném výběru, počítá se pomocí kvadrátů rozdílů pozorovaných hodnot od celkového průměru:

$\mathrm {S_{T}} =\sum _{i=1}^{k}\sum _{j=1}^{n}\left(Y_{ij}-{\bar {y}}\right)^{2}$

Tento odhad variability je funkce pozorovaných hodnot statistikou, která má své vlastní rozdělení pravděpodobnosti − i proto následně můžeme říci, že za platnosti $H_{0}$ má $S_{T}$ chí-kvadrát distribuci s určitým počtem stupňů volnosti roven $n-1$.

2. Skupinový součet čtverců (tzv. group sum of squares), $S_{A}$ = charakterizuje variabilitu mezi skupinovými průměry. Spočítat ho lze pomocí součtu kvadrátů rozdílů průměrů od celkového průměru:

$\mathrm {S_{A}} =\sum _{i=1}^{k}n_{i}\left({\bar {y}}_{i}-{\bar {y}}\right)^{2}$

Analogicky i statistika $S_{A}$ má své chí-kvadrát rozdělení pravděpodobnosti, v tomto případě jsou ale stupně volnosti rovny $k-1$.

3. Reziduální počet čtverců (tzv. residual sum of squares), $S_{A}$ = charakterizuje variabilitu v rámci jednotlivých skupin. Jeho hodnota je rovna součtu kvadrátů rozdílů pozorovaných hodnot od jednotlivých průměrů daných skupin:

$\mathrm {S_{e}} \sim \sum _{i=1}^{k}\sum _{j=1}^{n}\left(Y_{ij}-{\bar {y_{i}}}\right)^{2}$

Důležitým je zmínit statistiku $F$ (Fisherovo rozdělení), která je testovou statistikou pro analýzu rozptylu. V případě neplatnosti nulové hypotézy bude výsledná hodnota statistiky $F$ větší než 1. Počítá se jako podíl rozdílu mezi skupinami a rozptylu uvnitř skupin. Abychom ale $H_{0}$ mohli zamítnout, musíme znát kvantil rozdělení $F(k-1,n-1)$, jenž je příslušný určité hladině významnosti testu $\alpha$.

Po dosazení dostáváme následující výsledky:

ANOVA pro váhu

Zdroj variability	Součet čtverců	Počet stupňů volnosti	Průměrný čtverec	Statistika F	p-hodnota
Mezi skupinami	6457,6	2	3228,8	23,978	<0,001
Uvnitř skupin	2827,8	21	134,7
Celkem	9285,3	23

ANOVA pro věk

Zdroj variability	Součet čtverců	Počet stupňů volnosti	Průměrný čtverec	Statistika F	p-hodnota
Mezi skupinami	4063,08	2	2031,54	17,774	<0,001
Uvnitř skupin	2400,25	21	114,30
Celkem	6463,33	23

Finální tabulkou by bylo porovnání jednotlivých průměrů s uvedením p-hodnoty, například:

Finální tabulka pro interpretaci výsledků

Proměnná	Pacienti s infekční hepatitidou	Pacienti s autoimunitní hepatitidou	Pacienti s toxickou hepatitidou	p-hodnota
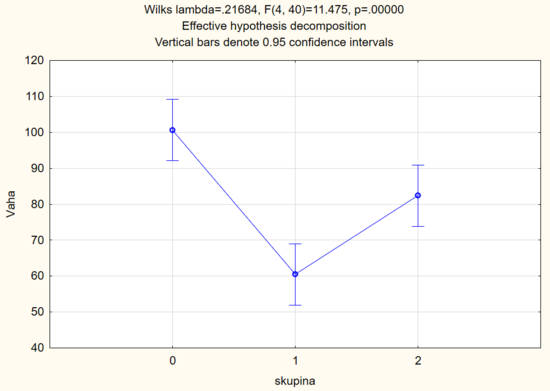
Váha v kg (průměr)	100,6	60,5	82,4	<0,001
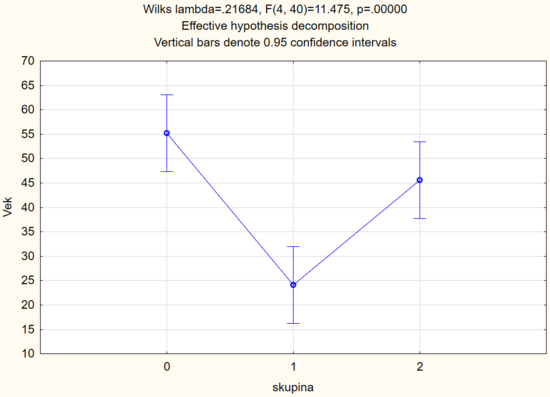
Věk v letech (průměr)	55,3	24,1	45,6	<0,001

Post-hoc analýzy

Je zřemé, že samotná p-hodnota vycházející z analýzy rozptylu více skupin neříká, jaké konkrétní proměnné (jejich rozptyly) se nejvíce liší. Pokud přijímáme $H_{1}$ na základě signifikantní p-hodnoty, je to vhodné zjistit. K účelu testování jednotlivých dvojic tedy využíváme tzv. post-hoc testy, které jsou v podstatě obdobou t-testu pro potřeby ANOVA. Nejčastěji se pro post-hoc analýzy využívá Fisherova LSD testu.

Odkazy

Související články

• Studentův t-test
• Portál:Zdravotnická statistika
• Normální rozdělení
• Testování statistických hypotéz

Externí odkazy

• ANOVA (česká wikipedie)
• Portál matematické biologie Masarykovy univerzity
• Výukový text o analýze rozptylu
• Výpočet Fisherova LSD testu, v anglickém jazyce.

Použitá literatura

• KLASCHKA, Jan. Studentův t-test [přednáška k předmětu Zdravotnická statistika 1,2, obor Všeobecné lékařství, 1. LF Univerzita Karlova]. Praha. 10.5.2011. 

• WOOLSON, Robert F. a William CLARKE. Statistical Methods for the Analysis of Biomedical Data. 2. vydání. New York : John Wiley & Sons. Inc., 2002. 368 s. ISBN 9780471394051.