Testy normality

Mnoho statistických metod (např. Studentův t-test) předpokládá, že základní soubor má normální rozdělení. Není-li tento předpoklad splněn, nelze danou metodu použít. K určení, zda lze rozdělení dat považovat za normální, slouží testy normality (např. Shapirův-Wilkův test). Většina statistického softwaru implementuje nějakou formu testů normality.

Je třeba si uvědomit, že zkoumané soubory často normální rozdělení nemají. Například schopnosti jsou v populaci rozloženy normálně, ale známky na vysvědčení jsou zpravidla vychýlené směrem k lepším hodnocením.

Níže budeme grafická znázornění pro testy normality aplikovat na hodnoty hmotnosti celkem 70 pacientů. Pro ilustrativní případy ji rozdělíme na dvě stejně velké skupiny, kdy jedna z nich bude mít hodnoty normálně rozložené a druhá nikoliv. Jejich demografické informace (tedy charakteristiky polohy a charakteristiky variability hodnot) uvádíme v tabulce:

Charakteristiky souboru
Rozdělení	Celkový počet hmotností	Průměr	Medián	Minimum	Maximum	Mezikvartilové rozpětí	Rozptyl	Směrodatná odchylka
Normální	35	71,11	78	54	104	21	181,81	13,48
Nenormální	35	73,63	68	12	168	48	1751,36	41,85

Zkuste již na základě těchto dat určit, jaké charakteristiky jsou zřejmými indikátory nenormálního rozdělení a proč jsou tedy v praxi užívané.

Grafické metody[upravit | editovat zdroj]

Jednoduchý způsob, jak alespoň přibližně odhadnout, zda data mají normální rozdělení, je sestrojení histogramu. O něco přesnější je použití Q-Q grafu (kvantil-kvantil) nebo P-P grafu (pravděpodobnost-pravděpodobnost). Q-Q graf je vhodnější pro testování normality na krajích rozdělení, zatímco P-P graf více zdůrazňuje odchylky od normálního rozdělení poblíž střední hodnoty.

Histogram[upravit | editovat zdroj]

Histogram je graf, který se sestrojí tak, že na vodorovnou osu nanášíme hodnoty sledované veličiny a na svislou osu jejich četnosti. Je-li zkoumaná veličina spojitá (tzn. nabývá-li nekonečně mnoha hodnot), rozdělíme osu na intervaly a četnosti určíme jako počty pozorovaných hodnot v těchto intervalech. Optimální počet intervalů lze určit podle tzv. Sturgesova pravidla. Při normálním rozdělení souboru by měl histogram připomínat Gaussovu křivku.

Histogramy pro testování normality a porovnání mezi normálním a nenormálním rozdělením jednotlivých hodnot, v našem případě jsme k tomu využili hmotnosti pacientů v kilogramech. Oba grafy jsou proloženy Gaussovou křivkou (červeně). Na ose y jsou zaneseny frekvence a na ose x jsou zaneseny hodnoty četností sledované veličiny.

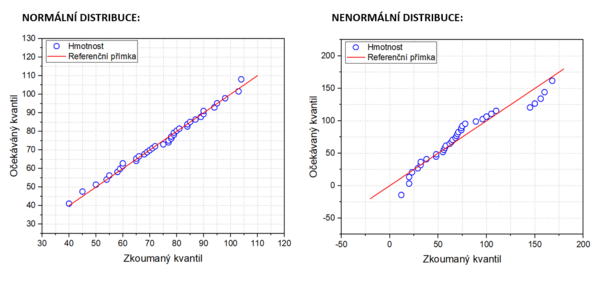
Q-Q graf[upravit | editovat zdroj]

Princip této metody spočívá v tom, že na jednu osu nanášíme kvantily hypotetického normálního rozdělení a na druhou osu kvantily zkoumaného souboru. V případě normálního rozdělení leží všechny body grafu na přímce.

Q-Q graf normálně a nenormálně rozdělených hodnot hmotností, které jsme otestovali pomocí histogramu výše. Referenční přímka uvádí Gaussovu křivku, hodnoty hmotností jsou modré kroužky.

P-P graf[upravit | editovat zdroj]

Postup při sestrojování P-P grafu je podobný jako u Q-Q grafu. Na jednu osu nanášíme hodnotu kumulativní distribuce hypotetického normálního rozdělení a na druhou osu hodnotu kumulativní distribuce zkoumaného souboru. Opět v případě normálního rozdělení budou body ležet na přímce.

P-P graf normálně a nenormálně rozdělených hodnot hmotností užitých v předchozích testech normality. Analogicky opět referenční přímka uvádí Gaussovu křivku, hodnoty hmotností jsou modré kroužky.

Ověření normality výpočtem[upravit | editovat zdroj]

Existuje řada testů, které se liší silou a náročností provedení. Patří mezi ně např. Shapirův-Wilkův, Andersonův-Darlingův, Kolmogorovův-Smirnovův, Lillieforsův a další. Test se obvykle neprovádí ručně, ale kvůli velké náročnosti se výpočty provádějí na počítači. Příklad výpočtu v programu R (testovaný soubor je v proměnné x):

> shapiro.test(x)

Shapiro-Wilk normality test

data: x

W = 0.9685, p-value = 0.8762

Je-li p-hodnota větší než 0,05 normalita se nezamítá.

Hrubý odhad[upravit | editovat zdroj]

Chceme-li posoudit normalitu rozdělení pouze orientačně, můžeme porovnat aritmetický průměr s mediánem. podle některých autorů^[zdroj?]by se neměly lišit více než o 10 %.

Odkazy[upravit | editovat zdroj]

Související články[upravit | editovat zdroj]

Použitá literatura[upravit | editovat zdroj]

NETOLICKÁ, Veronika. Testy normality. Přírodovědecká fakulta Univerzity Palackého v Olomouci : Katedra matematické analýzy a aplikací matematiky, 2008,

KASAL, Pavel a Marie HLADÍKOVÁ. Koutek pro statistiky amatéry. Pelikán : akademický bulletin 2. LF UK [online]. 1995, roč. 3, no. 3, s. -, dostupné také z <http://stary.lf2.cuni.cz/projekty/pelikan/peli0395/statis1.htm>.

WOOLSON, Robert F. a William CLARKE. Statistical Methods for the Analysis of Biomedical Data. 2. vydání. New York : John Wiley & Sons. Inc., 2002. 368 s. ISBN 9780471394051.