Elektrokardiografie/Fyzika: Porovnání verzí
m (spřesnení) |
m (obrazok) |
||
| Řádek 35: | Řádek 35: | ||
== Hrudní svody == | == Hrudní svody == | ||
[[Soubor:ECG-Wilson-R.svg|náhled|'''Wilsonova svorka''' - referenční elektroda pro hrudní svody]] | |||
Na hrudník umístňujeme v klasickém 12-svodovém EKG šest hrudních elektrod (potenciály značme <math>\phi_1</math> až <math>\phi_6</math>). | Na hrudník umístňujeme v klasickém 12-svodovém EKG šest hrudních elektrod (potenciály značme <math>\phi_1</math> až <math>\phi_6</math>). | ||
Hrudní svody jsou '''unipolární''', referenční elektrodou je Wilsonova svorka. Pro napětí každého hrudního svodu (značíme <math>U_1</math> až <math>U_6</math>) tedy platí: | Hrudní svody jsou '''unipolární''', referenční elektrodou je '''Wilsonova svorka'''. Pro napětí každého hrudního svodu (značíme <math>U_1</math> až <math>U_6</math>) tedy platí: | ||
:<math>U_1=\phi_1-\phi_W</math> | :<math>U_1=\phi_1-\phi_W</math> | ||
| Řádek 42: | Řádek 43: | ||
:<math>U_6=\phi_6-\phi_W</math> | :<math>U_6=\phi_6-\phi_W</math> | ||
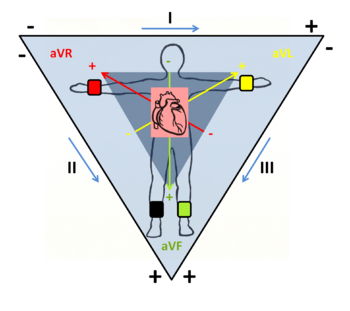
Dohromady tedy dostáváme dvanáct svodů. Končetinové svody (I, II, III, aVR, aVL, aVF) sledují změny potenciálu ve '''frontální rovině''', hrudní svody (V<sub>1</sub> až V<sub>6</sub>) v '''transversální rovině'''. | Dohromady tedy dostáváme dvanáct svodů. Končetinové svody (I, II, III, aVR, aVL, aVF) sledují změny potenciálu ve '''frontální rovině''', hrudní svody (V<sub>1</sub> až V<sub>6</sub>) v '''transversální rovině'''. | ||
== Vznik signálu == | == Vznik signálu == | ||
Verze z 21. 12. 2024, 19:34
Fyzikální veličina, kterou při EKG vyšetření snímáme, je elektrické napětí (někdy též ). Elektrické napětí je definováno jako rozdíl eleketrických potenciálů mezi dvěma body, tedy:
Jednotkou elektrického napětí je volt (v EKG milivolt).
Elektroda je kovový vodič v kontaktě s kůží, jehož potenciál snímáme. V EKG je dělíme na aktivní (explorativní) a referenční (indiferentní).
Svod tvoří kombinace (dvojice) elektrod, ze kterých snímáme napětí. Alespoň jedna z nich musí být elektrodou aktivní. Jsou-li obě elektrody svodu aktivní, hovoříme o bipolárním svodu. Je-li jedna elektroda aktivní a druhá referenční, pak mluvíme o unipolárním svodu. Svod si můžeme představit jako citlivý voltmetr, nebo osciloskop. Zdůrazňujeme, že mluvit o napětí jednoho bodu nemá smysl (je nulové pro každý bod), proto i unipolární svody měří napětí mezi vícero elektrodami.
Standardní EKG obsahuje 10 elektrod. Čtyři jsou končetinové, jedna z nich je zemnící a neslouží k snímaní. Šest elektrod je hrudních. Kombinácí těchto elektrod je sestaveno 12 svodů, z toho šest končetinových a šest hrudních. Pro umístnění elektrod viz Elektrokardiografie#12svodové EKG.
Končetinové svody
Končetinové svody využívají končetinových elektrod. Potenciály na těchto elektrodach označme pro pravou horní, levou horní a levou dolní končetinu. Bipolární končetinové svody se standardně značí římskými číslicemi a jejich napětí lze pomocí potenciálů vyjádřit následovně:
Z uvedených definicí okamžitě vidno, že jednotlivá napětí na končetinových svodech nejsou nezávislá, nýbrž platí tzv. Einthovenův zákon podle kterého:
Spojením všech tří končetinových elektrod přes stejné rezistory (5 k) vzniká tzv. Wilsonova svorka. Potenciál na Wilsonově svorce je aritmetickým průměrem potenciálů tří končetinových elektrod a je považován za konstantní.
V současnosti se unipolární končetinové svody měří nikoliv vůči Wilsonově svorce, ale vůči zbylým dvěma elektrodám (po rozpojení měřené končetiny z Wilsonovy svorky). Dostáváme tedy další tři svody, které nazýváme Goldbergovy (pseudounipolární, zesílené, augmented):
Tato napětí rovněž nejsou nezávislá. Platí:
Tyto úvahy lze posunout ješte dál. Ze všech šesti končetinových svodů jsou ve skutečnosti pouze dva unikátní. Stačí tedy znát napětí na dvou libovolných svodech a všechny zbylé končetinové svody (napětí) lze jednodznačně dopočítat.
Hrudní svody
Na hrudník umístňujeme v klasickém 12-svodovém EKG šest hrudních elektrod (potenciály značme až ). Hrudní svody jsou unipolární, referenční elektrodou je Wilsonova svorka. Pro napětí každého hrudního svodu (značíme až ) tedy platí:
Dohromady tedy dostáváme dvanáct svodů. Končetinové svody (I, II, III, aVR, aVL, aVF) sledují změny potenciálu ve frontální rovině, hrudní svody (V1 až V6) v transversální rovině.
Vznik signálu
Z těchto 12 svodů EKG dostáváme 12 záznamů napětí v čase. Výchylka (napětí) na EKG křivce závisí v každém čase na velikosti a směru elektrického dipólového momentu srdce. Ten vzniká součtem mnoha elementárních dipólů na mikroskopické úrovni. Při dané velikosti je el. napětí na svodu největší, když míří tento vektor podél spojnice elektrod daného svodu. Naopak el. napětí je nulové, když je el. dipólový moment kolmý na daný svod. Matematicky přesněji je napětí dané skalárním součinem:
Kde je vektor daného svodu (lead vector) a je úhel mezi vektory a . Připomeňme, že ale což odpovídá textu výše. Elektrický dipólový moment srdce se mění rychle s časem. Výsledkem je, že u unipolárních svodů se šíření depolarizace směrem k elektrodě zaznamenává (podle dohody) jako pozitivní výchylka, naopak šíření depolarizace od elektrody jako negativní výchylka. Při repolarizaci to platí obráceně. U bipolárních svodů je znaménko výchylky dané polaritou svodu, v předešlé rovnici tedy vektorem (viz. Einthovenův trojúhelník nebo definice přes napětí). Prohozením elektrod v jednom svodu se změní znaménko naměřeného napětí (stejně jako u voltmetru), EKG křivka tohoto svodu se tedy převrátí "vzhůru nohama".
Elektrická osa srdeční
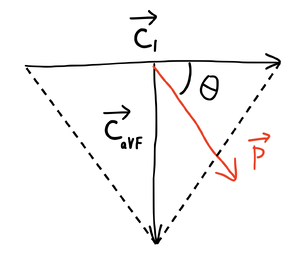
Elektrickou osu srdeční vyjadřujeme úhlem mezi elektrickým dipólovým momentem srdce a horizonální osou (té odpovída svod I, tedy jeho vektor ). Pokusíme se tento úhel spočítat pomocí napětí ze svodů I a aVF. Tyto si vyjadřime jako skalární součiny se svodovými vektory, viz předešlý odstavec.
Úhel je naše neznámá. Napětí v aVF si rovněž vyjádřime jako skalární součin. Povšimněme si, že úhel mezi vektorem a svodovým vektorem aVF je doplňek úhlu . Z goniometrie víme, že sinus úhlu je cosinus jeho doplňku, proto platí:
Podělme nyní druhou rovnici první.
V posledním kroku jsme využili faktu, že tangens je podíl sinu a cosinu. Velikost svodového vektoru aVF vůči svodovému vektoru I je jako výška vůči straně rovnostranného trojúhelníku. Z Pythagorovy věty je tedy rovna , je-li strana rovna 1. Využitím tohoto faktu a přeuspořádáním předešlé rovnice dostáváme výsledný vztah pro určení úhlu elektrické osy srdeční:
Konkrétní řešení pro daný úhel závisí na kvadrantu, v kterém se osa pohybuje, proto vyjadřujeme úhel pouze implicitně.
Tohoto výpočtu využívá i Kalkulačka srdeční osy.