Schrödingerova rovnice

Schrödingerova rovnice je matematická rovnice popisující kvantový systém, např. elektron v atomu.

V klasickém (makroskopickém) světě používáme pro popis pohybu těles klasickou mechaniku, založenou na Newtonových zákonech. Pro popis mikroskopického světa však nutno použít kvantovou mechaniku. Schrödingerova rovnice má v kvantové mechanice obdobnou roli jako Newtonův druhý zákon v klasické mechanice. Řešením Schrödingerovy rovnice je vlnová funkce (wave function) $\psi$ (psí), která plně charakterizuje kvantový systém.

V některých případech (např. při zkoumání stavby atomů) nás nezajímá časový vývoj systému, jen jeho stacionární stav. Pak používáme tzv. stacionární (časově nezávislou, bezčasovou) Schrödingerovu rovnici (time-independent Schrödinger equation), která má tvar:

${\hat {H}}\psi =E\psi {}$

kde ${\hat {H}}$ je Hamiltonův operátor, který vyjadřuje celkovou energii systému, $E$ je energie daného stavu.

Schrödingerova rovnice je nerelativistická, tedy uvažuje rychlost částic mnohem menší než rychlost světla ve vakuu (a všechno, co z toho plyne). Pro relativistický popis kvantových systémů slouží Klein-Gordonova rovnice.

Význam vlnové funkce

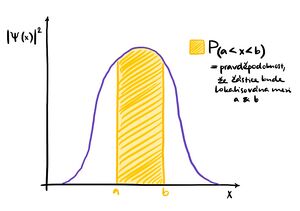
V mikroskopickém světě není možné částici přesně lokalizovat v prostoru, neboť platí Heisenbergovy relace neurčitosti. Lze u ní určit jenom pravděpodobnost $P$, že bude v nějaké části prostoru. Vlnová funkce udává právě tuto pravděpodobnost. Například pravděpodobnost, že částice v jednorozměrném prostoru bude lokalizovaná mezi body $a$ a $b$ je dána

$P(a<x<b)=\int _{a}^{b}|\psi (x)|^{2}\;dx$

Geometrické znázornění významu vlnové funkce

Geometricky tedy plocha pod křivkou $|\psi (x)|^{2}$ odpovídá pravděpodobnosti výskytu částice (viz obrázek). Vlnová funkce je obecně komplexní funkce.

Vlnová funkce elektronu v atomu (v molekule) se nazývá atomový (molekulový) orbital.