Fórum:Testy/Analýza výsledků

Dopady výsledků testování mohou mít v praxi zásadní důsledky – např. rozhodnutí o přijetí, rozhodnutí o udělení atestace nebo o udělení titulu. Použijeme-li nevhodné testy, závěry učiněné z jejich výsledků mohou být zavádějící. Kvalita použitých testů a jejich položek je proto zásadní a je důležité ji pravidelně kontrolovat.

Jaké vlastnosti by měl mít kvalitní znalostní test? V první řadě by měl měřit znalost, kterou měřit chceme. Dále by měl měřit co nejpřesněji a výsledky by měly být reprodukovatelné, zadáme-li studentovi jinou verzi téhož testu. Testy a jednotlivé položky by měly být spravedlivé a neměly by zvýhodňovat některé skupiny. Jednotlivé položky by měly mít vhodnou obtížnost a měly by mít schopnost dobře rozlišovat mezi různými úrovněmi znalostí studentů. Jak ověřit, zda náš test všechny tyto vlastnosti splňuje? Mnohé nám napoví analýza výsledků testu.

Jak analýzu výsledků provést? Prvním krokem analýzy výsledků by měl být souhrnný popis a vhodné grafické vyobrazení celkových výsledků všech studentů. Taková sumarizace se často vyžaduje při vykazování výsledků nebo pro sledování vývoje výsledků u stejného testu v průběhu let. Ukážeme si ale, že může být také prvním nástrojem k identifikaci problémů testu, např. při nežádoucím prozrazení („vynesení“) části úloh.

V dalším kroku je důležité prozkoumat vlastnosti testu jako celku, především jeho reliabilitu neboli spolehlivost, a jeho validitu, tedy zda měří znalost, kterou měřit chceme. Ke kvalitě celého testu přispívají jednotlivé položky (otázky v testu), je proto potřeba sledovat také vlastnosti jednotlivých položek a nabízených distraktorů. Tato položková analýza v sobě zahrnuje odhady obtížnosti a citlivosti jednotlivých položek. Je důležitá také pro tvorbu dvou nebo více srovnatelných verzí testu.

V následujícím textu se převážně budeme věnovat klasickým odhadům vlastností testu a jeho položek. Klasické odhady mají však svá omezení. V první řadě tyto odhady závisí na úrovni znalosti testované populace. To je na závadu, používáme-li položky nebo celé testy pro skupiny studentů, které se od sebe výrazněji liší (např. v případě sdílení položkových bank). Nemůžeme pak nekriticky převzít popis určité položky, který například říká, že jde o položku snadnou – pokud test aplikujeme na jiné skupině studentů, kteří se třeba vzdělávají jiným systémem, může pro ně tatáž položka být naopak velmi obtížná. V případě vyššího počtu testovaných studentů je tak vhodné použít k odhadům vlastností položek a úrovní znalostí studentů složitějších odhadů, tzv. teorie odpovědi na položku (item response theory, IRT). IRT umožní modelovat vlastnosti položky a celého testu pro různé úrovně znalosti studentů.

Nepředpokládáme, že by čtenář měl umět sám provést všechny níže uvedené analýzy. Záměrně uvádíme i složitější analýzy a rozebíráme výhody, aby čtenář získal představu o různých možnostech ověřování kvality testů. Cílem je, aby čtenář byl o metodách informován a věděl, co lze zjistit pomocí dostupného softwaru, nebo ve spolupráci se specialistou – statistikem.

Tip: Jak na to?

Obecně platí, že popis výsledků nebo klasickou položkovou analýzu lze poměrně snadno provést svépomocí v tabulkovém procesoru jako je např. MS Excel. Na složitější analýzy, např. odhady validity pomocí regresních modelů, ale také na IRT odhady vlastností položek je již zapotřebí statistického softwaru. K dispozici je celá škála programů a většinou je potřeba zakoupit jejich licenci (SPSS, Statistica, SAS, NCSS, Splus a mnoho jiných). Z volně šiřitelných zmiňme alespoň prostředí R. Ze softwarů specializujících se na znalostní testy pak lze uvést např. software ITEMAN . Analýzu výsledků je také možné automatizovat. V případě počítačového testování je dobré vyžadovat co nejkvalitnější analýzu vlastností testu a jednotlivých položek po softwaru použitém k testování.

Tip: Jak na to?

Popis a grafické zobrazení výsledků

Prvním krokem analýzy by vždy měl být popis výsledků dosažených v testu pomocí souhrnných statistik a vhodného grafické vyobrazení. Souhrnný pohled na výsledky nám dá první představu o vlastnostech testu, může ale také upozornit na jeho problémy. Patrně každého zkoušejícího zajímá, jaký byl nejlepší dosažený výsledek a zda někdo dosáhl maximálního počtu bodů. Jaký je nejhorší výsledek? A pokud má několik studentů test zcela nesprávně, čím je to způsobeno, nenastala jen někde procesní chyba v hodnocení (například obodování testu podle šablony pro jinou variantu)? Celkovou obtížnost testu můžeme dále popsat průměrným počtem bodů. Seřadíme-li výsledky vzestupně, obtížnost můžeme popsat také prostřední hodnotou (tzv. mediánem). Zadáváme-li stejný test opakovaně, je dobré sledovat, jak se průměrný výsledek vyvíjí v letech. Můžeme tak například odhalit, že kvalita studentů se rok od roku snižuje. Nebo naopak, že si vedou studenti rok od roku lépe. Ve druhém případě je ale na místě otázka, zda je to lepšími znalostmi studentů, nebo tím, že test je již prozrazený (vynesený).

Směrodatná odchylka vypovídá o rozptýlenosti výsledků. Jak již víme, přibližně 95 % výsledků bude ležet ± 2 směrodatné odchylky od průměru (viz také kapitola z-skór studenta). To ovšem pouze v případě, že se výsledky řídí normálním (neboli tzv. Gaussovým) rozdělením – což by obecně měly, ale je potřeba to také ověřit.

Tabulka popisných statistik pro celkové výsledky může vypadat např. takto:

Tab. 8.1 Tabulka popisných statistik

minimální možný počet bodů	0
maximální možný počet bodů	100
dosažené minimum	27
dosažené maximum	99
průměr	68,8
medián	68,0
směrodatná odchylka	15,3

Pokud se průměr od mediánu výrazněji liší, může to indikovat nesymetrii výsledků, potažmo nenormalitu dat. Šikmost rozdělení může souviset s celkovou přílišnou jednoduchostí či obtížností testu. Je-li test například příliš snadný a větší množství výsledků se pohybuje u maximálního možného počtu bodů (víc bodů získat nelze), delší „chvost“ je nalevo.

Pro celkový výsledek studenta v testu se odborně používá termín hrubý skór. Většinou je hrubý skór počítán jako součet bodů za jednotlivé položky; někdy však může být počítán složitěji.

Graficky lze rozdělení hrubých skórů ve skupině testovaných studentů posoudit pomocí histogramu, který jsme zahlédli již v předchozích částech textu. Histogram je sloupcový graf, v němž výška sloupců vyjadřuje četnost sledované veličiny v daném intervalu. Lze jej chápat jako odhad hustoty rozdělení vědomostí v populaci. V běžném případě očekáváme, že se rozdělení znalostí řídí normálním rozdělením. Pro posouzení, zda tomu tak skutečně je, lze histogram proložit křivkou normálního rozdělení (přičemž střední hodnotu a rozptyl odhadujeme z dat), viz obr. 8.1.

Obr. 8.1 Histogram celkových skóre u studentů a jím proložená křivka normálního rozdělení

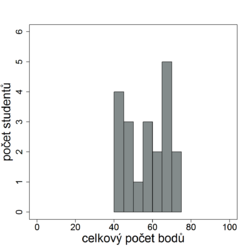
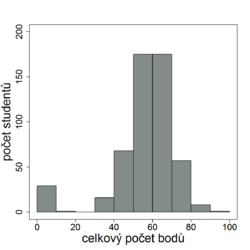
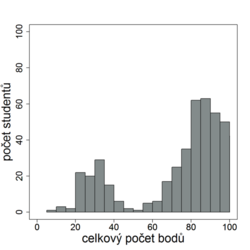
Histogram nemusí odpovídat křivce normálního rozdělení, máme-li malý počet studentů (viz obr. 8.2a). Máme-li studentů dostatek, histogram by křivce normálního rozdělení odpovídat měl. V opačném případě je to upozorněním na možné problémy: Naznačuje-li graf nějaké neobvyklé výsledky, tzv. odlehlé hodnoty (viz obr. 8.2b, např. několik málo jedinců má počet bodů mnohem nižší nebo mnohem vyšší než ostatní), je potřeba se zamyslet nad jejich příčinami. Nebyl v těchto případech test obodován podle špatné šablony? Alarmující je také dvouvrcholový histogram (viz obr. 8.2c). Naznačuje, že námi testovaní studenti jsou ve skutečnosti směsí dvou nebo více různých skupin s různými vlastnostmi a patrně také s různými podmínkami pro úspěch v testu. Důvodem mohou být různí vyučující, různí cvičící, ale také např. vynesení testu. Takové skutečnosti je pak potřeba brát v potaz i v dalších níže uvedených analýzách (a např. pro případ dvou nebo více skupin je potřeba buď výsledky skupin analyzovat samostatně, nebo použít složitějších modelů).

• Příklady histogramů pro podezřelá rozdělení celkových skóre
• 

  Obr. 8.2a Histogram v případě malého počtu studentů

• 

  Obr. 8.2b Histogram v případě odlehlých hodnot

• 

  Obr. 8.2c Histogram v případě dvou skupin s různými vlastnostmi