1. termodynamický zákon

1. termodynamický zákon vyjadřuje zákon zachování energie v termodynamickém systému. Matematicky:

$\Delta U=Q-W$

kde $\Delta U$ je celkový přírůstek vnitřní energie dané soustavy, $Q$ je celkové teplo, přijaté systémem od okolí, a $W$ je celková práce, kterou systém vykonal na okolí.

Často se setkáme s vyjádřením v diferenciálním tvaru:

$\mathrm {d} U=\mathrm {d} Q-\mathrm {d} W$

U rovnice v diferenciálním tvaru se nejedná o hodnoty změněné za dobu trvání celého děje, ale za nekonečně krátký časový úsek.

Fyzikální interpretace

Jedná se o případ zákon zachování energie:

Energie, o kterou vnitřní energie systému vzroste, nemůže vzniknout z ničeho, ale musí být systému dodána zvenčí (tj. jeho okolím), a to ve formě tepla Q nebo mechanické práce W. Anebo, jinak řečeno, při výměně energie mezi systémem a okolím energie nevzniká ani nezaniká:

$\Delta U-Q+W=0$

Aplikace 1. termodynamického zákona

První termodynamický zákon má veliké užití při popisu dějů v ideálním plynu, ve kterém mohou probíhat různé (v praxi využívané) děje. Aby byl jejich popis co nejsnazší a podstata co nejzřetelnější, zavedeme obecné parametry soustavy, na které budou jednotlivé děje popisovány:

Soustava je

1. uzavřená (nemůže s okolím vyměňovat hmotu)
2. neizolovaná (může s okolím vyměňovat energii)
3. obsahuje 1 mol ideálního plynu.

Díky prvním dvěma podmínkám můžeme uvažovat formulaci 1.TZ uvedenou výše, díky třetí podmínce můžeme zanedbat člen $n$ - tj. látkové množství (protože $n=1$) - a díky poslední podmínce nemusíme uvažovat ztráty způsobené vnitřním třením.

Uvažujme speciální děje, během kterých tato soustava nemění jednu ze svých stavových veličin, tj. $\mathrm {d} X=0$, kde $X$ je daná stavová veličina.

Izochorický děj

Izochora

Děj, při němž nedochází ke změně objemu, tj. $\mathrm {d} V=0$, nazýváme izochorický (z řec. isos - stejný a choros - prostor).

Platí $\mathrm {d} W=p\mathrm {d} V=0$. Z prvního termodynamického zákona po dosazení vyplývá $\mathrm {d} Q=\mathrm {d} U$

a tedy vešekeré dodané teplo se spotřebuje na zvýšení vnitřní energie $\Delta U$.

Křivku závislosti $p=p(V)$ při ději izochorickém nazýváme izochora.

Izotermický děj

Izotermy ideálního plynu

Děj, při němž nedochází ke změně teploty, tj. $\mathrm {d} T=0$, nazýváme izotermický (z řec. isos - stejný a therme - teplo).

Platí $\mathrm {d} U=C_{V}\mathrm {d} T=0$, kde $C_{V}$ je molární tepelná kapacita daného plynu za konstatního objemu.

Z prvního termodynamického zákona po dosazení vyplývá $\mathrm {d} Q=-\mathrm {d} W$

a tedy vešekeré dodané teplo se spotřebuje na vykonání práce.

Křivku závislosti $p=p(V)$ při ději izotermickém nazýváme izoterma.

Izobarický děj

Izobara

Děj, při němž nedochází ke změně tlaku, se jmenuje děj izobarický (z řec. "isos" - stejný a "baros" - tíha). Tedy $\mathrm {d} p=0$.

Ze stavové rovnice nám vychází matematický popis izobarického děje v ideálním plynu $V/T=konst.$, což je tzv. Gay-Lussacův zákon.

Pro výpočet práce vykonané plynem platí $\mathrm {d} W=p\mathrm {d} V$, po dosazení do rovnice prvního termodynamického zákona dostaneme jeho podobu pro izobarický děj. $\mathrm {d} Q=\mathrm {d} U+p\mathrm {d} V$

Křivku závislosti $p=p(V)$ při izobarickém ději nazýváme izobara. Vzhledem ke konstantní hodnotě tlaku, práce vykonaná plynem se dá odečíst z grafu jako plocha pod křivkou ohraničená začáteční a výslední hodnotou objemu plynu. Tato plocha je grafickým zobrazením rovnice $\mathrm {d} W=p\mathrm {d} V$.

Teplo přijaté ideálním plynem při izobarickém ději se rovná součtu přírůstku jeho vnitřní energie a práce, kterou plyn vykoná.

Z hlediska platnosti prvního termodynamického zákona je tento děj nejkomplikovanější. Žádná z veličin vystupujících v prvním termodynamickém zákoně nebude nulová (u izochorického děje je nulová práce vykonaná ideálním plynem, u izotermického děje je nulová změna vnitřní energie plynu během daného děje). Praktické využití izobarického děje stejně jako ostatních termodynamických dějů najdeme například u vznětových motorů (Dieselův cyklus).

Adiabatický děj

Adiabata

Při ději adiabatickém platí $\mathrm {d} Q=0$, tedy mezi plynem a okolím buď neprobíhá tepelná výměna (jako v izolovaných soustavách), nebo děj proběhne tak rychle, že se žádná tepelná výměna nestihne uskutečnit. Tudíž je děj velmi komplikovaný na uskutečnění. Reálné děje bývají na pomezí mezi dějem izotermickým a adiabatickým (Polytropický děj). Entropie se u adiabatického děje nemění.

Po dosazení do rovnice prvního termodynamického zákona

 $\mathrm {d} W=-\mathrm {d} U$

je vidět, že soustava koná práci na úkor vnitřní energie.

Tato rovnice by se dala dále upravovat, z čeho bychom dostali $pV^{\kappa }=$ konst. Přičemž $\kappa$ je Poissonova konstanta a dá se vyjadřit z rovnice $\kappa =c_{p}/c_{V}$.

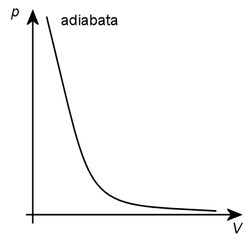
Takové vyjádření stanovuje závislost mezi proměnnými $p$ a $V$ a tím pádem dovoluje adiabatický děj vyjádřit také na diagramu (p, V). Tato křivka se jmenuje adiabata. Podobá se izotermě, má však strmější průběh, který odvodíme z rovnice izotermy $pV^{1}=$ konst. přičemž Poissonova konstanta $\kappa$ je větší než jedna.

Při adiabatickém stlačování plynu v nádobě se působením vnější síly na píst koná práce, teplota plynu a jeho vnitřní energie se zvětšuje. Při adiabatickém rozpínání koná práci plyn, teplota plynu i jeho vnitřní energie se zmenšuje. Adiabatického rozpínání se používá k dosažení nízkých teplot, adiabatického stlačování se používá u vznětových motorů: adiabatickou kompresí se zvýší teplota vzduchu na zápalnou teplotu nafty, která se po vstříknutí do tohoto vzduchu sama vznítí.

Odkazy

Související články

• Termodynamické věty

Zdroje

• MARŠÁK, Zlatěk. Termodynamika a statistická fyzika. 3. vyd. Praha: Vydavatelství ČVUT, 1995, s. 23-25. ISBN 80-01-01401-0.

• Multimediální encyklopedie fyziky (MEF), 2006-2013, Jaroslav Reichl, Martin Všetička http://fyzika.jreichl.com/