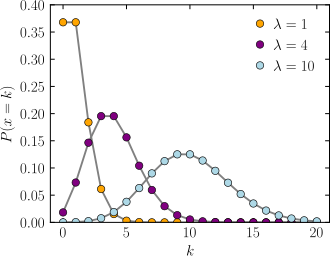
Poissonovo rozdělení

Poissonova distribuce (rozdělení) je statistické rozdělení náhodné proměnné určující počet výskytů událostí v průběhu času, přičemž k těmto událostem dochází náhodně a na sobě vzájemně nezávisle. U Poissonova rozdělení je typické, že se podle něj řídí četnosti událostí, které ale jsou poměrně vzácné − mají tedy velmi malou pravděpodobnost výskytu (například se může jednat o počet krvácivých událostí u sledovaných osob za 100 osobo-roků aj.). Občas je tedy možné narazit na méně typické označení této konkrétní distribuce, a to rozdělení řídkých jevů.

Samotná náhodná veličina má rozdělení: $Po(\lambda )$.

Předpoklady

Aby se náhodná veličina řídila Poissonovým rozdělením, musí být splněny následující podmínky:

1. určitá událost může nastat v jakémkoliv časovém okamžiku;
2. počet událostí v průběhu času závisí pouze na časovém intervalu − nezáleží ale na jeho počátku či konci;
3. $\lambda$ se považuje za střední hodnotu počtu výskytů jevů za časovou jednotku.

Náhodná veličina $\lambda _{i}$ závisí na $k$ veličinách značených $x_{i}$, kde $i=1,2,...,k$. Finální zápis by tedy byl $x_{1},x_{2},...,x_{k}$, což jsou veličiny, které nazýváme kovariáty. Úkolem Poissonova rozdělení je najít vztahy mezi nimi. Abychom tyto vztahy byli schopni nalézt, definujeme funkci:

$\lambda _{i}=\lambda (x_{i})=\lambda (x_{1},...,x_{k}).$

Vzorec

$P(X=x)={\frac {\lambda ^{x}}{x!}}\mathrm {e} ^{-\lambda }$

e představuje Eulerovo číslo.

Příklad

Výskyt rakoviny žlučníku

Uvažujme, že se u mužské populace, věkově ohraničené 35 až 40 lety, za rok v jednom kraji vyskytne pět případů rakoviny žlučníku. Za proměnnou X považujeme počet případů tohoto onemocnění v průběhu roku. Protože víme, že se ročně vyskytne pět případů rakoviny žlučníku, proměnná X bude následovat Poissonovu distribuci ve tvaru $\lambda =5(1)=1$. Naším cílem je zjistit pravděpodobnosti toho, že se rakovina v daný rok 1) nevyskytne, 2) vyskytne jednou, 3) vyskytne dvakrát:

1. $P(X=0)={\frac {e^{-5}}{0!}}\mathrm {(5)} ^{0}={e^{-5}}=0,00674$
2. $P(X=1)={\frac {e^{-5}}{1!}}\mathrm {(5)} ^{1}={5e^{-5}}=0,03369$
3. $P(X=2)={\frac {e^{-5}}{2!}}\mathrm {(5)} ^{2}={12,5e^{-5}}=0,08422$

Z těchto výsledků nám plyne, že praděpodobnost nepřítomnosti onemocnění v daný rok je necelé jedno procento, pravděpodobnost jediného výskytu rakoviny žlučníku kolem tří procent a výskyt tří případů 8,4 %.

Výskyt leukémie

Druhým příkladem si ukážeme, jakým způsobem musíme postupovat pro výpočet předpokládaných případů událostí, pokud chceme reflektovat velikost sledované populace a časového intervalu.

Předpokládejme, že anuální výskyt leukémie je 11,2 případů na 100 000 osob. Pokud bychom těchto 100 000 osob sledovali po dobu jednoho roku, jaká bude pravděpodobnost, že nezaznamenáme žádné nové případy tohoto onemocnění? A jaká bude tato pravděpodobnost, pokud bude vztažena na pouhých 1000 osob?

Obě skupiny je nutné si adekvátně rozdělit. Pro 100 000 osob je výskyt leukémie 11,2, tedy:

$P(X=0)={\frac {e^{-11,2}}{0!}}\mathrm {(11,2)^{0}} =0,0000137$

Pro skupinu 1000 osob je výskyt nových případů roven 0,112 ((11,2/100 000)x1000). Proto bude vzorec vypadat následovně:

$P(X=0)={\frac {e^{-0,112}}{0!}}\mathrm {(0,112)^{0}} =0,89$

Pravděpodobnost toho, že se leukémie nevyskytne v naší hypotetické populaci čítající 100 00 jedinců, je hluboko pod jedním procentem. Naopak u populace o 1000 jedincích je tato pravděpodobnost 89 %.

Odkazy

Související články

• Atributivní riziko
• Absolutní riziko
• Relativní riziko
• Incidence
• Normální rozdělení
• Metaanalýza
• Konfidenční interval

Externí odkazy

Skripta o Poissonově distribuci s ukázkovými grafy, v anglickém jazyce

Použitá literatura

• WOOLSON, Robert F. a William CLARKE. Statistical Methods for the Analysis of Biomedical Data. 2. vydání. New York : John Wiley & Sons. Inc., 2002. 368 s. ISBN 9780471394051.